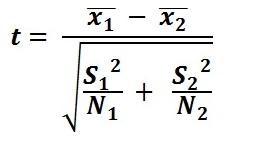StavelotNews.eu

Ceci avec deux buts en tête :

1. Simplement pour partager avec vous ces données. Dans des articles qui vont suivre, diviser des valeurs, comme des revenus, par le nombre d'habitants va nous servir à mieux comprendre certains chiffres. Un peu comme dans un article précédent, le P.I.B. et le P.I.B. par habitant étaient présentés.
2. Présenter quelques outils statistiques, et que vous connaissiez probablement déjà, sur ces mêmes tableaux.

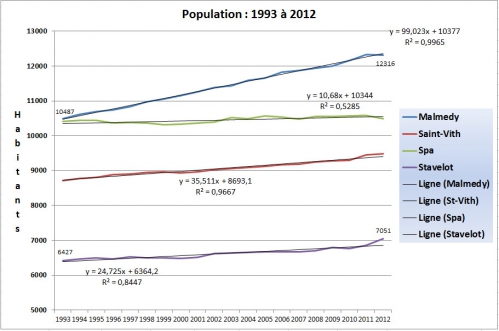
Voici deux façons de présenter des changements dans la population avec le temps. Ci-dessous, des equations linéaires, présentées avec un coéfficient de corrélation. Ceci nous donne une idée pour répondre à la question : "La population, augment-elle tout simplement avec le passage du témps?" A Malmedy (ligne bleu du dessus) R² = 0,9965, qui nous apprend que le simple passage des années explique 99,65% de la variability que l'on retrouve d'une année à l'autre dans la population Malmédienne.  Une ligne plus bas (la verte) la valeur de R² = 0,5285, nous suggère que la variabilité dans les chiffres de population à Spa, est expliquée par le passage du temps seulement 52,9% du temps. Cette relation est plus forte à Saint-Vith (R²=0,9667), et un peu moins fort à Stavelot (R²=0,8447).

Comment se servir des équations pour prédire la population dans une année, je laisse pour un autre article.

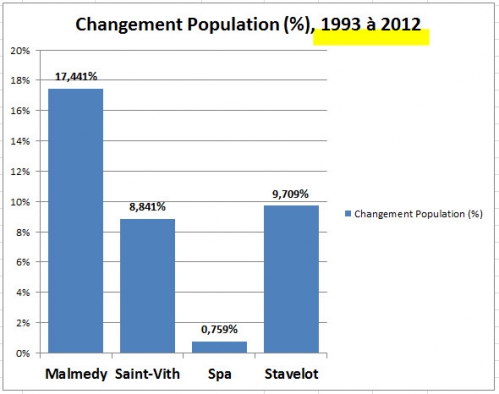
Une autre façon de présenter ces changements avec le temps est le suivant : la population en 2012 - moins la population en 1993, et ce résultat divisé par la valeur de population en 1993.  Et voici les résultats ci-dessous, exprimés en pourcentages.

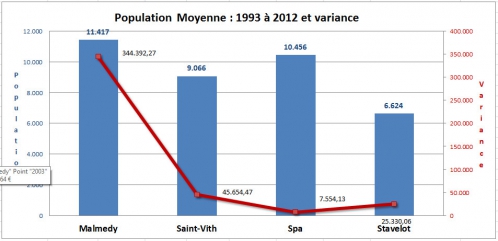
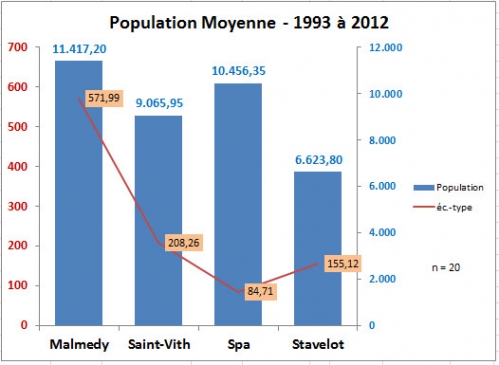
Regardons de plus près les valeurs des variances et les écarts-types associés à ces valeurs moyennes de population :

Vous avez peut-être plus l'habitude de voir une moyenne présentée avec sa valeur d'écart-type. La variance est une mesure servant à caractériser la dispersion d'un échantillon ou d'une distribution. Elle indique de quelle manière la série statistique ou la variable aléatoire se disperse autour de sa moyenne.  Une variance de zéro signale que toutes les valeurs sont identiques. Une petite variance est signe que les valeurs sont proches les unes des autres alors qu'une variance élevée est signe que celles-ci sont très écartées.

Pour calculer la variance d'une série statistique ou d'une variable aléatoire, on calcule les écarts entre la série, ou la variable, et sa moyenne, puis on prend la moyenne de ces écarts élevés au carré.

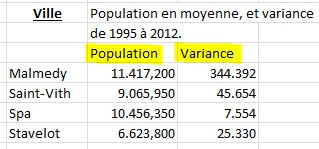
La racine carrée de la variance s'appelle l'écart type. Donc, le tableau ci-dessus, qui présentent des valeurs de variance, et celui ci-dessous, qui présente des valeurs d'écart-types, et dans les deux cas avec les moyennes de populations, nous renseignent la même chose ... (ceci la ligne rouge dans chaque tableau). La variance dans la moyenne des populations (et forcément l'écart-type) est plus importante à Malmedy, que pour Spa, Saint-Vith et Stavelot. Plus de variabilité dans les chiffres de population d'une année à l'autre implique plus d'entrées et sorties.

La variance nous permet aussi de choisir d'autres outils pour comparer les moyennes. Si ces valeurs sont proches, mais la variance entre les deux plus importante, certains outils seraient un meilleur choix que d'autres pour faire cette comparaison : Ceci pour décider si les moyennes sont identiques ou pas.

Ci-dessous, les moyennes des populations de 1993 à 2012. Ces moyennes sont chaque fois présentées avec leur écart-type. On peut aussi noter sur ce tableau, "n = 20" qui vient simplement confirmer le nombre de variables qui est repris dans chaque moyenne (20 années de chiffres de population). Comment faire pour décider si ces moyennes sont les mêmes ou différentes? En les regardant, on dirait par exemple que Saint-Vith et Spa sont pas loins d'être identique en population dans l'interval étudié. Ou ont peut chosir de dire : "Spa à plus de mille personnes en plus que Saint-Vith en moyennes dans ces années." Les regarder à l'oeil ansi, ne prend pas compte de la variabilité dans ces moyennes. Cette dispersion est reprise dans les écart-types dans ce tableau, même que la variance aurait pu servir aussi bien. (La forme de la ligne rouge est identique dans les deux tableaux).

Q : Comment faire pour tester mathématiquement si ces moyennes sont identiques ( = pas de différence dans ces populations), ou pas ?

R : Avec un test nommé "Student's t-test" qui sert à mesurer les dispersions et chevauchements de ces deux distributions de populations. Enonçons ceci comme l'hypothèse nulle (que l'on dit en statistique) : "Il n'y à pas de différence entre les moyennes de population à Saint-Vith et Spa." Et avec quel niveau de certitude ? Souvent nous allons prendre une valeur de p<0,05, qui veut dire que la probabilité que notre conclusion est erronée et en dessous de 5 chances sur 100 essais.

Donc :       Moyenne     écart-type     n

                   9.065,95       208,26        20      (Saint-Vith)

                  10.456,35        84,71        20      ( Spa )

Voici l'équation pour le test de Student :

est ici, x = les moyennes; s = les écart-types; et n = le nombre de variables.

Entre parenthèses ...

Je trouve cela intéressant, que "Student" était un pseudonyme. L'équation fut développée en 1908 par William S. Gossett. Mais Monsieur Gossett avait déjà tant publié dans le domaine des statistiques qui'l se sentait un peu gêné de publier encore une fois sous son propre nom. Donc, il a inventé un pseudonyme, «Student». La plupart des personnes qui se servent de tels outils se souviennent de "Student's t-test," mais pas de Gossett.

Puisque les écart-type (208,26 et 84,71 sont assez différents, une correction de Welch est appliqué à notre résultat (pourquoi? ... ça c'est une autre histoire, mais en bref, pour rendre notre conclusion mathématiqe encore plus discriminante). 

Voici les résultats :

 t = 27,657  avec 25 "degrees of freedom" qui donne un résultat de p < 0,0001.

Donc, "l'hypothèse nulle" qu'il n'y a aucune différence entre ces deux moyenne est rejeter, car la probabilité que cette différence dans les moyennes est apparu au hazard, est moins d'une chance sur 10.000 !  Peu probable ! Ces moyennes sont très différentes.

Deuxième exemple : Malmedy et Stavelot ...

Donc :        Moyenne     écart-type     n

                   11.417,20      571,99        20      (Malmedy)

                     6.623,80      155,12        20      ( Stavelot )

Résultat ?  t = 36,578 avec 21 "degrees of freedom" qui donne p< 0,000001

Moins d'une chance sur 1.000.000 que ces deux moyennes ont été prise de la même distribution de populations. Elles sont différentes.

Cet exercice devient plus intéressant quand les valeurs sont plus prôches, et vous cherchez à les distinguer. Pour savoir, les valeurs de "t" et de "p" dans nos deux exemples ce jour sont énormes, sans aucun doute.

Et "degrees of freedom," qui se traduit "degrés de liberté," ... c'est quoi ça ? Je signale de suite que cela n'a rien à faire avec une question politique ni les droits de l'homme ! 

En statistiques le degré de liberté (ddl) désigne le nombre de variables aléatoires qui ne peuvent être déterminées ou fixées par une équation (notamment les équations des tests statistiques). Si cela vous laisse dans l'incertitude, une autre définition est fournie par Walker, H. M. dans son article «Degrees of freedom.» publié en 1940 dans Journal of Educational Psychology, (Vol 31(4), Apr 1940, 253-269. doi: 10.1037/h0054588). : «the number of observations minus the number of necessary relations among these observations.» Qui se traduit ...

Le nombre de degré de liberté est égal au nombre d'observations moins le nombre de relations entre ces observations. On pourrait remplacer l'expression «nombre de relations» par «nombre de paramètres à estimer».

Par exemple si l'on cherche deux chiffres dont la somme est 12, aucun des deux chiffres ne peut être directement déterminé par la simple équation .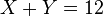

 peut être choisi arbitrairement, mais alors pour Y  il n'y a plus le choix. Ainsi, si vous choisissez 11 comme valeur pour X, Y vaut obligatoirement 1. Il y a donc deux variables aléatoires 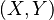, mais un seul degré de liberté.

Que faire de tout cela? Une fois que la correctes methode pour calculer ces degrés de liberté est trouvé (car en fonction du test choisi c'est parfois n - 1 ou n - 2 par exemple), on sort une valeur : 21 dans le dernier exemple. Dans le passé, on prennait son cahier de tableux statistiques en main. On tournait à la page avec des valeurs de "p" pour le statistique "t" de Student. On descendait dans la colonne avec l'en-tête "df" (donc, degrés de liberté) et une fois la valeur de (dans notre cas) 21 identifiée, on lisait la valeur de "p." Maintenant, cela se fait à l'ordinateur qui permet d'y arriver plus vite à la réponse, et souvent avec moins de compréhension de ce que l'on est en train de faire ...

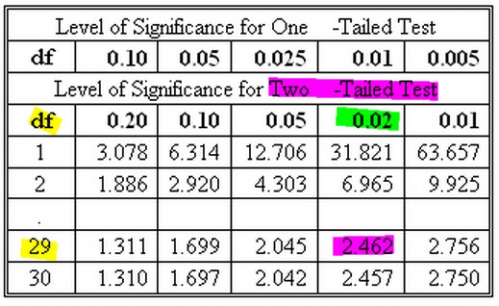
Voici une image pour vous en donner le sens :

Dans ce cas, 29 degrés de liberté (jaune) et une valeur de "Student's t - test" de 2,462 (rose) se trouve en dessous d'une valeur de "p" = 0,02 (en vert). Si le tableau ne présentait pas nos valeurs exactes, il fallait faire une extrapolation pour calculer la vraie valeur de "p." Passons, car ce détail n'ajoute rien à notre présentation.  Donc dans leur étude (je ne sais de quoi il s'agissait) une comparaison de valeurs moyennes, (qui n'apparaissent pas dans ce tableau), avec 29 degrés de liberté et une valeur t = 2,462 offre une valeur de "p" = 0,02. Cela veut dire qu'il existe 2 chances sur 100, que les moyennes (qui sembleraient d'être différentes), ne le sont pas, et que cette différence apparente s'est présentée par hazard. Et de tout cela, le besoin d'avoir une valeur pour degré de liberté. Et comme vous pouvez le constater, une très haute valeur de "t" est nécessaire quand la valeur de "df" est basse, pour arriver à la même valeur de probabilité, "p." C'est logique. Le plus de fois que l'on fait la mesure d'une variable (par exemple ici, 30 fois au lieu de 2 fois), le plus facile est-il de se rapprocher de la vérité.

"p" = "probabilité" d'un certain résultat. En science médicale, une valeur de p < 0,05 (p en dessous de 0,05) est presque toujours sélectionnée comme celle significatif ou importante. Si les chercheurs ont démontrés que leurs résultats ont moins de 5 chances sur 100 d'être apparus par hazard ... "c'est bon." Mais trop s'y attacher à cette valeur veut dire aussi qu'un résultat important est parfois abandonné comme sans importance. Parfois 1 fois ou 2 fois sur 10 (p < 0,10; p < 0,20) comme probabilité qu'un résultat provient du hazard, nous laisse quand-même encore 9 fois ou 8 fois sur 10 que cela n'est pas le cas. Quand on se trouve avec des résultats près de ce seuil de p < 0,05 mais sans passer dans la zone "importante," cela demande "relooker" et repenser les variables dans nos expériences, repenser comment les données sont mesurées, et essayer de développer de meilleurs contrôles pour extirper les forces du hazard de notre travail.  

Assez pour l'instant, si pas trop ...

Et si vous n'aviez pas d'idée de la population Stavelotaine et des villes avoisinantes avant ...,  ce n'est plus le cas.